前回の続き。

読んでいないかたは、前回のエントリーから先にどうぞ。

わかりやすく説明してみます。

最初にカードを選んだとき
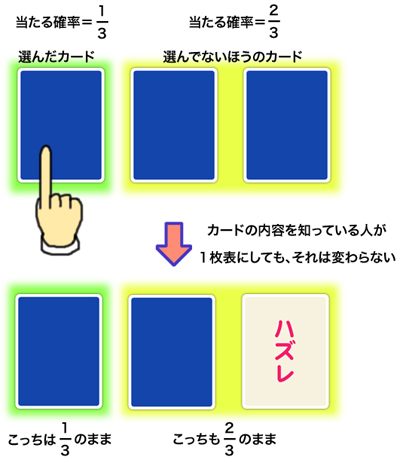
そのカードがハートのＡ＝当たりである確率は、１／３ですよね。
３枚のうち、どれかが当たりなわけですから。

てことは、選んでいない２枚のほう
これを仮に「選んでない２枚側」と呼びます。
その２枚のどちらか＝「選んでない２枚側」に当たりがある確率は？
そう、２／３ですよね。

そして、僕は、カードの内容を知ってますので
「選んでない２枚側」の２枚から１枚、ハズレを表にしました。

１枚、ハズレが表になりましたが
「選んでない２枚側」の、当たり確率は２／３であることに変わりません。

同じく、「選んだほうのカード」の当たり確率も変化ありません。
１／３のままです。

てことは、「選んだほうのカード」のまま（１／３）にしておくよりも
カードを変えて、「選んでない２枚側」（２／３）にしたほうが
当たる確率は、かなりアップするわけです。

ということでした。

「選んでないグループ」から、１枚ハズレが表になって
裏の状態のカードが２枚になったからって
５０％：５０％じゃ、ないんですよね。

……で、実は、ここからが言いたかったこと。

上の説明で、理屈は「わかって」いただけたと思うのですが
「納得」がしずらいんですよね。

「まあ、確かにそうかも……でもなあ」という感じ。

或いは

「いや、うーん。そうは思えないなあ」とか。

で、どうやったら、納得できるか？
これが大切だなあと思ったのです。

理屈じゃないんですよね、やっぱり。

納得するほうほうは簡単。
実際に３枚のトランプ（じゃなくてもよいわけですが）で
やってみるといいですよ。

「変えたとき」と「変えないとき」の、両方をやる必要はありません。
「必ず変える」というルールでやってみればよいわけです。
そのとき、ハズレだったら、「変えない」ほうがよかったわけで
「当たり」か「ハズレ」かを、チェックしておけば、わかります。

で、カミさんにやってもらいました。
実際に、トランプ３枚ゲームを、２０回ほど。

すると、ほんとに変えたほうが、当たりがかなり多いのです。

みなさんも、納得ができなかったら
トランプでもなんでも、そういうものがあれば、できますので。

実際に、２０回くらいやってみると
変えたほうが、２／３という値にかなり近くなるのです。
ハズレは（＝変えない場合と同じ）、１／３となります。

……と、やっていただければ、実感はできると思うのですが
それでもまだ、納得いかない、というかたのために。
こういうふうに考えたら、わかると思います。

トランプを３枚ではなく
ぜんぶ使ったとして、考えてみましょう。

トランプをＡ〜Ｋまで（１３枚）
ハートもクローバーもダイアもスペードも（×４）使います。
さらに、その５２枚に、ジョーカー２枚を加えて
５４枚、ぜんぶ使います。
（ジョーカー１枚しかない場合もありますが、５４枚として話を進めますね）

さあ、５４枚あります。

この５４枚から、どれか１枚を、まず選びます。
どれかを選ぶとして…………まぁ、当たらないでしょ。

確率がどう、とかいうのは、もう置いといていいです。
５４枚から１枚、当たりを選ぶんだから、そりゃ当たらない。
３枚とは違って、当てるのは、かなり難しい。

逆にいうと、選んだカード以外の、５３枚のカードのほうに
当たりがある可能性は、かなり高いですよね。
選んでない、残りのほうに当たりがありそうですよね？

では、あなたが選んだカード以外の５３枚
＝選んでいない５３枚のカードを、１枚１枚、表にしていきます。

もう大サービスです。
また１枚、また１枚と、候補を消していきます。

また１枚、また１枚と……。どんどんなくなります。
そして、最後には、選んでない５３枚のカードから、１枚だけを残して。

……って、考えたら、その１枚のほうが
「当たり」だっていう気がしませんか？

これで、たぶん、納得いただけたと思いますが
実際に、やってみるほうが、よいかと思います。

友達とやってみると、盛り上がるでしょう。
恋人や、配偶者、子どもがいるかたは、よいコミュニケーションになります。
あえて、自分が先に１人でテストしてしまわないで
一緒に「そうかなあ？」「あっ、ほんとだ！」というのは
なかなか楽しいものですよ。

ぜひ。